.
Latest Post
Hiển thị các bài đăng có nhãn NGÔ BẢO CHÂU. Hiển thị tất cả bài đăng
Hiển thị các bài đăng có nhãn NGÔ BẢO CHÂU. Hiển thị tất cả bài đăng
22:21
Chủ tịch HĐQT Tinh Vân "hỏi vặn" GS Châu
Written By kinhtehoc on Thứ Bảy, 7 tháng 4, 2012 | 22:21
Chuyên mục
NGÔ BẢO CHÂU
22:25
http://www.aivaky.com/2012/03/ai-va-ky.html
Địa chỉ "Ai và Ky" sách mới của GS Ngô Bảo Châu Và Nguyễn Phương Văn
Written By kinhtehoc on Thứ Bảy, 24 tháng 3, 2012 | 22:25
http://www.aivaky.com/2012/03/ai-va-ky.html
Chuyên mục
NGÔ BẢO CHÂU
02:14
Where I’m from- Ngô Bảo Châu
Written By kinhtehoc on Thứ Năm, 15 tháng 3, 2012 | 02:14
I am from books, from Hyperion Books and mysteries
I am from the one bedroom apartment
(the apartment as small as a doll house and
as cozy as you are sitting next to the fireplace)
I am from the orchids
That flutters and flies when the wind blows
I am from the one bedroom apartment
(the apartment as small as a doll house and
as cozy as you are sitting next to the fireplace)
I am from the orchids
That flutters and flies when the wind blows
I am from the hard workers and overachievers
From the Le’s and Tran’s
I am from the debates and neatness
From stories to morals
The lesson learned from when I was small
From the Le’s and Tran’s
I am from the debates and neatness
From stories to morals
The lesson learned from when I was small
I am from watching my mom pray
Then praying myself to Buddha
The one that guides me to become a better person
Then praying myself to Buddha
The one that guides me to become a better person
I am from Vietnam
I am from the spring rolls and noodles
I am from the death of my great-grandmother
And the tears that came along
I am from the spring rolls and noodles
I am from the death of my great-grandmother
And the tears that came along
I am from Manhattan
Where my memories were made
With my family and friends
The love that bring us together
The happiness and laughter
The sadness and pain
That we go through together
Memories
I am from the memories
Where my memories were made
With my family and friends
The love that bring us together
The happiness and laughter
The sadness and pain
That we go through together
Memories
I am from the memories
I am from my family who made me a better person
With the lessons my parents taught me
The respect I have for myself and others
I am from my friends who gave me my personality
The weird one, the nerd
But the friends that made me proud of who I am
I am from my family and friends
With the lessons my parents taught me
The respect I have for myself and others
I am from my friends who gave me my personality
The weird one, the nerd
But the friends that made me proud of who I am
I am from my family and friends
Chuyên mục
NGÔ BẢO CHÂU
02:09
Tết Hà Nội và Margarita- Thơ Ngô Bảo Châu
NGÔ BẢO CHÂU
Tết Hà Nội chìm trong những cơn tắc đường miên man. Mặt mũi ai cũng có vẻ đăm chiêu nhiều hơn là hân hoan chờ năm mới tới. Bạn bè gặp nhau trò chuyện thâu đêm rồi lại chia tay nhau trong lòng ấm áp hơn một chút. Nhìn ra ngoài trời tối đen như mực chợt nhớ đến Margarita :
Trái đất này buổi tối sao buồn quá
Ánh sao xa rọi sáng đọt lúa vàng
Bà phù thủy cưỡi chổi cười mê sảng
Lạc mất rồi mặt trời ngày đã qua
Ánh sao xa rọi sáng đọt lúa vàng
Bà phù thủy cưỡi chổi cười mê sảng
Lạc mất rồi mặt trời ngày đã qua
Chuyên mục
NGÔ BẢO CHÂU
01:33
Thơ - Ngô bảo Châu
Mặc dù chưa được phép của bác Châu nhưng Phúc xin mạn phép chép thơ của bác lên đây để mọi người cùng đọc mong bác đại xá :d
1) Cuội
Rong chơi để rơi mất tuổi,
Mải đùa với bướm chú Cuội mất tên
Mải đùa với bướm chú Cuội mất tên
2) Con đường là mục đích
Có một con đường ta đi,
Giá chi không bao giờ tới đích
Giá chi không bao giờ tới đích
3) Godel
Định lý đủ, Định lý thiếu
Biết bao nhiêu thì đủ
Sao bao nhiêu cũng thiếu
Ông Godel xin kiếu.
Biết bao nhiêu thì đủ
Sao bao nhiêu cũng thiếu
Ông Godel xin kiếu.
4) Cháo chay qui nạp (cảm hứng từ chữ của 5xu)
Lô-gic bần đạo không rành
Cháo chay qui nạp lại thành cháo khê
Xơi vào lại hóa cháo mê
Qui đi nạp lại biết về lối nao ?
Cháo chay qui nạp lại thành cháo khê
Xơi vào lại hóa cháo mê
Qui đi nạp lại biết về lối nao ?
5) Proust và Goldmund
Ngày xưa có một ông tây
Cắn một miếng bánh viết vài ngàn trang
Loay hoay đi tìm thời gian
Tìm ra con rắn trên giàn su su
Cắn một miếng bánh viết vài ngàn trang
Loay hoay đi tìm thời gian
Tìm ra con rắn trên giàn su su
6) Cái chết của mùa thu (dịch thơ của Jean Richepin)
Ngọn gió bắc
Quật vào nách
Thu cà khổ
Lủi một mạch
Quật vào nách
Thu cà khổ
Lủi một mạch
Ngọn gió bắc
Cuộn thu lu
Trong thùng rượu
Thu đã chết
Cuộn thu lu
Trong thùng rượu
Thu đã chết
Chuông đã nguyện
Như lời than
Trong điệp khúc
Cuối cùng
Như lời than
Trong điệp khúc
Cuối cùng
Của cuộc vui
Vĩnh biệt ruộng nho
Đã hái hết rồi.
Vĩnh biệt ruộng nho
Đã hái hết rồi.
7) Cất nỗi buồn vào đâu ?
Cất nỗi buồn vào tài khoản tiết kiệm
Để ngày mới là niềm vui tươi rói
Còn cho ta rảnh chân thanh thản
Rảo bước với thời gian …
Để ngày mới là niềm vui tươi rói
Còn cho ta rảnh chân thanh thản
Rảo bước với thời gian …
Em hỏi anh sao anh dại thế
Cất nỗi buồn vào tài khoản tiết kiệm
Nhỡ rồi nó, lãi mẹ đẻ lãi con
Cất nỗi buồn vào tài khoản tiết kiệm
Nhỡ rồi nó, lãi mẹ đẻ lãi con
Em yêu ơi đằng nào chúng ta cũng dại rồi
Đã chót buồn vui
Đã chót uống gió của bầu trời
Đã chót buồn vui
Đã chót uống gió của bầu trời
Để lãi mẹ đẻ lãi con cũng tốt
Chờ khi nào anh chết
Em đem hóa vàng tuốt tuồn tuột cho anh.
Chờ khi nào anh chết
Em đem hóa vàng tuốt tuồn tuột cho anh.
8. Dấu guốc (dịch lời ca Notre Sentier của Felix Leclerc)
Con đường mòn nằm bên bờ suối
Bị xéo nát bởi những luống cầy
Cho tôi biết khi nào em tới
Tôi sẽ đợi dưới cây bạch dương
Bị xéo nát bởi những luống cầy
Cho tôi biết khi nào em tới
Tôi sẽ đợi dưới cây bạch dương
Tổ chim lạnh tanh và rách nát
Ngọn gió bắc thổi lá đi đâu
Chim én thôi bay
Sóc nâu thôi nhảy
Chân em vết guốc
Loãng thành vũng nước
Ngọn gió bắc thổi lá đi đâu
Chim én thôi bay
Sóc nâu thôi nhảy
Chân em vết guốc
Loãng thành vũng nước
Con đường mòn nằm bên bờ suối
Bị xéo nát bởi những luống cầy
Cho tôi biết khi nào em tới
Tôi sẽ đợi dưới cây bạch dương
Bị xéo nát bởi những luống cầy
Cho tôi biết khi nào em tới
Tôi sẽ đợi dưới cây bạch dương
Tôi khâu lại tổ chim
Với cặp lá lặng im
Nếu thấy bên bờ rào
Đôi quạ đen hôm nào
Liệu em có ném vào vũng nước
Ký ức cùng cả hai chiếc guốc
Với cặp lá lặng im
Nếu thấy bên bờ rào
Đôi quạ đen hôm nào
Liệu em có ném vào vũng nước
Ký ức cùng cả hai chiếc guốc
Nào em đến khóc bên bờ suối
Rồi đập vụn tình yêu của tôi
Quên rồi ngày hạ, quên luôn mặt trời
Quên cả tên tôi, lẫn cây bạch dương.
Rồi đập vụn tình yêu của tôi
Quên rồi ngày hạ, quên luôn mặt trời
Quên cả tên tôi, lẫn cây bạch dương.
9) Bài hát con sên đi đưa ma (dịch thơ của Jacques Prevert)
Một tối thu, hai con sên đi đưa ma một chiếc lá
Cái vỏ ốc nhuộm cho đen, còn ăng ten cuộn khăn trắng
Nhưng tiếc rằng khi tới nơi, thì mùa xuân tới trước rồi
Những chiếc lá mới quyên sinh, nay hồi sinh xanh mượt mà
Hai con sên, vì chậm chân mà đến muộn, thấy tủi thân
Ông mặt trời nở nụ cười nói khe khẽ, này sên ơi
Ngồi xuống đây, làm cốc bia cho khỏi khát
Rồi tối nay, nếu cậu thích lấy xe buýt đi Pa ri
Dọc trên đường phong cảnh đẹp, rồi thì dẹp trò đưa tang
Đi đưa ma mắt trẵng dã, ôm quan tài thật buồn bã
Hãy tươi nỏ mầu cuộc sống cùng cây cỏ và chim muông
Cùng nhau ca, ca thật vang, vang bài ca của mùa hạ
Rồi cùng uống, cùng cụng ly trong mê ly của cuộc sống
Hai con sên quay về nhà, thấy cảm động, thấy hạnh phúc
Hơi phê phê, hơi say say, nhưng thật may
ở trên cao, có trăng sao, dẫn đường …
Cái vỏ ốc nhuộm cho đen, còn ăng ten cuộn khăn trắng
Nhưng tiếc rằng khi tới nơi, thì mùa xuân tới trước rồi
Những chiếc lá mới quyên sinh, nay hồi sinh xanh mượt mà
Hai con sên, vì chậm chân mà đến muộn, thấy tủi thân
Ông mặt trời nở nụ cười nói khe khẽ, này sên ơi
Ngồi xuống đây, làm cốc bia cho khỏi khát
Rồi tối nay, nếu cậu thích lấy xe buýt đi Pa ri
Dọc trên đường phong cảnh đẹp, rồi thì dẹp trò đưa tang
Đi đưa ma mắt trẵng dã, ôm quan tài thật buồn bã
Hãy tươi nỏ mầu cuộc sống cùng cây cỏ và chim muông
Cùng nhau ca, ca thật vang, vang bài ca của mùa hạ
Rồi cùng uống, cùng cụng ly trong mê ly của cuộc sống
Hai con sên quay về nhà, thấy cảm động, thấy hạnh phúc
Hơi phê phê, hơi say say, nhưng thật may
ở trên cao, có trăng sao, dẫn đường …
10) Quan họ
Yêu nhau cắt tóc cho nhau
Về nhà mẹ hỏi tóc đâu mất rồi
Tóc kia đổi lấy một lời
Cắt đi còn lại một đời nhớ nhung
Về nhà mẹ hỏi tóc đâu mất rồi
Tóc kia đổi lấy một lời
Cắt đi còn lại một đời nhớ nhung
11) Tết Hà nội và Margerita
Trái đất này buổi tối sao buồn quá
Ánh sao xa rọi sáng đọt lúa vàng
Bà phù thủy cưỡi chổi cười mê sảng
Lạc mất rồi mặt trời ngày đã qua
Ánh sao xa rọi sáng đọt lúa vàng
Bà phù thủy cưỡi chổi cười mê sảng
Lạc mất rồi mặt trời ngày đã qua
12) Đồng luân
Có ai đi hết mặt cầu
Đồng luân mấy nẻo về đâu thoát đời.
Đồng luân mấy nẻo về đâu thoát đời.
Chuyên mục
NGÔ BẢO CHÂU
01:23
Phạm trù và đồng luân (2)-NGÔ BẢO CHÂU
GS Ngô Bảo Châu
Phải thừa nhận là “Phạm trù và đồng luân (1)” rất khó hiểu, không chỉ đối với người đọc mà cả đối với người viết  Tôi đã mắc khuyết điểm là kéo bạn đi quá nhanh, đi từ những cái bạn biết là không gian tô pô, ánh xạ liên tục đến những chỗ mà cả bạn lẫn tôi và thực ra cả nhân loại chưa hiểu rõ, đó là đồng luân cấp cao.
Tôi đã mắc khuyết điểm là kéo bạn đi quá nhanh, đi từ những cái bạn biết là không gian tô pô, ánh xạ liên tục đến những chỗ mà cả bạn lẫn tôi và thực ra cả nhân loại chưa hiểu rõ, đó là đồng luân cấp cao.
Bây giờ là lúc bạn nhẩn nha quay chậm lại cuộn phim để níu kéo lại một chút gì hữu hình cho bạn. Bạn có một không gian tô pô 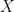 . Bạn xét các điểm của
. Bạn xét các điểm của 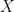 , rồi xét các đoạn thẳng trong
, rồi xét các đoạn thẳng trong 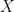 tức là các ánh xạ liên tục
tức là các ánh xạ liên tục ![{[0,1] \rightarrow X} {[0,1] \rightarrow X}](http://s0.wp.com/latex.php?latex=%7B%5B0%2C1%5D+%5Crightarrow+X%7D&bg=ffffff&fg=000000&s=0) , rồi các hình vuông trong
, rồi các hình vuông trong 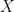 tức là các ánh xạ liên tục
tức là các ánh xạ liên tục ![{[0,1]^2 \rightarrow X} {[0,1]^2 \rightarrow X}](http://s0.wp.com/latex.php?latex=%7B%5B0%2C1%5D%5E2+%5Crightarrow+X%7D&bg=ffffff&fg=000000&s=0) , rồi hình vuông ba chiều (lập phương), rồi hình vuông
, rồi hình vuông ba chiều (lập phương), rồi hình vuông  chiều.
chiều.
Cố định một điểm qui chiếu  . Nhóm cơ bản
. Nhóm cơ bản  là nhóm các lớp tương đương (đồng luân) các đoạn thẳng xuất phát và kết thúc tại điểm
là nhóm các lớp tương đương (đồng luân) các đoạn thẳng xuất phát và kết thúc tại điểm  , tức là ánh xạ
, tức là ánh xạ ![{f:[0,1] \rightarrow X } {f:[0,1] \rightarrow X }](http://s0.wp.com/latex.php?latex=%7Bf%3A%5B0%2C1%5D+%5Crightarrow+X+%7D&bg=ffffff&fg=000000&s=0) với
với  . Nói cách khác thì
. Nói cách khác thì  là một ánh xạ liên tục từ hình tròn
là một ánh xạ liên tục từ hình tròn 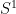 vào
vào  . Khi bạn buộc hai đầu mút của đoạn
. Khi bạn buộc hai đầu mút của đoạn ![{[0,1]} {[0,1]}](http://s0.wp.com/latex.php?latex=%7B%5B0%2C1%5D%7D&bg=ffffff&fg=000000&s=0) lại với nhau, nó trở thành cái gì đó giống như hình tròn.
lại với nhau, nó trở thành cái gì đó giống như hình tròn.
Phần tử đơn vị của  là lớp của ánh xạ hằng
là lớp của ánh xạ hằng ![{e:[0,1] \rightarrow X } {e:[0,1] \rightarrow X }](http://s0.wp.com/latex.php?latex=%7Be%3A%5B0%2C1%5D+%5Crightarrow+X+%7D&bg=ffffff&fg=000000&s=0) với
với  với mọi
với mọi ![{\alpha \in [0,1]} {\alpha \in [0,1]}](http://s0.wp.com/latex.php?latex=%7B%5Calpha+%5Cin+%5B0%2C1%5D%7D&bg=ffffff&fg=000000&s=0) . Đồng luân của
. Đồng luân của  với chính nó là một ánh xạ liên tục
với chính nó là một ánh xạ liên tục ![{f:[0,1] \times [0,1] \rightarrow X } {f:[0,1] \times [0,1] \rightarrow X }](http://s0.wp.com/latex.php?latex=%7Bf%3A%5B0%2C1%5D+%5Ctimes+%5B0%2C1%5D+%5Crightarrow+X+%7D&bg=ffffff&fg=000000&s=0) nhận giá trị
nhận giá trị  trên biên của hình vuông. Nói cách khác
trên biên của hình vuông. Nói cách khác 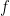 là một ánh xạ liên tục từ mặt cầu
là một ánh xạ liên tục từ mặt cầu  vào
vào  . Tưởng tượng hình vuông như một cái mù soa, khi bạn buộc biên của mù soa lại, nó trở thành cái gì đó giống như mặt cầu. Như vậy nhóm đồng luân cấp hai
. Tưởng tượng hình vuông như một cái mù soa, khi bạn buộc biên của mù soa lại, nó trở thành cái gì đó giống như mặt cầu. Như vậy nhóm đồng luân cấp hai  là nhóm các lớp tương đương (đồng luân) của các ánh xạ liên tục
là nhóm các lớp tương đương (đồng luân) của các ánh xạ liên tục  gửi một điểm qui chiếu của mặt cầu (nơi biên của hình vuông chập lại) lên điểm qui chiếu
gửi một điểm qui chiếu của mặt cầu (nơi biên của hình vuông chập lại) lên điểm qui chiếu  của
của 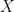 .
.
Chiều ba thì khó tưởng tượng hơn nhiều. Khi bạn “buộc” biên của hình lập phương lại thành một điểm, nó trở thành mặt cầu ba chiều  . Tất nhiên là khó tưởng tượng rồi, vì cả tôi và bạn đều chưa “nhìn” thấy mặt cầu ba chiều bao giờ. Nhưng dù sao bạn đã có đủ cơ sở đển tin rằng nhóm đồng luân
. Tất nhiên là khó tưởng tượng rồi, vì cả tôi và bạn đều chưa “nhìn” thấy mặt cầu ba chiều bao giờ. Nhưng dù sao bạn đã có đủ cơ sở đển tin rằng nhóm đồng luân  là nhóm các lớp tương đương (đồng luân) của các ánh xạ liên tục từ mặt cầu
là nhóm các lớp tương đương (đồng luân) của các ánh xạ liên tục từ mặt cầu 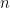 chiều
chiều  vào
vào  , gửi một điểm qui chiếu trên mặt cầu lên điểm qui chiếu
, gửi một điểm qui chiếu trên mặt cầu lên điểm qui chiếu  của
của 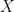 .
.
*****
Trong cái “phạm trù” nhắc đến trong bài trước, vật là các điểm của 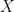 , mũi tên là các đoạn thẳng trên
, mũi tên là các đoạn thẳng trên 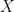 , mũi tên cấp 2 là các hình vuông trên
, mũi tên cấp 2 là các hình vuông trên 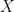 … Nhưng bạn còn chưa xét kỹ làm thế nào có thể hợp thành hai đoạn thẳng, hai hình vuông …
… Nhưng bạn còn chưa xét kỹ làm thế nào có thể hợp thành hai đoạn thẳng, hai hình vuông …
Bạn dễ hình dung cách hợp thành hai đoạn thẳng mà đoạn sau xuất phát nơi đoạn trước kết thúc. Cho ![{f_1:[0,1]\rightarrow X} {f_1:[0,1]\rightarrow X}](http://s0.wp.com/latex.php?latex=%7Bf_1%3A%5B0%2C1%5D%5Crightarrow+X%7D&bg=ffffff&fg=000000&s=0) với
với  ,
,  và
và ![{f_2:[0,1] \rightarrow X } {f_2:[0,1] \rightarrow X }](http://s0.wp.com/latex.php?latex=%7Bf_2%3A%5B0%2C1%5D+%5Crightarrow+X+%7D&bg=ffffff&fg=000000&s=0) với
với  ,
,  . Bạn có thể dựng
. Bạn có thể dựng  bằng cách chia đoạn
bằng cách chia đoạn ![{[0,1]} {[0,1]}](http://s0.wp.com/latex.php?latex=%7B%5B0%2C1%5D%7D&bg=ffffff&fg=000000&s=0) thành hai phần
thành hai phần ![{[0,1/2]} {[0,1/2]}](http://s0.wp.com/latex.php?latex=%7B%5B0%2C1%2F2%5D%7D&bg=ffffff&fg=000000&s=0) và
và ![{[1/2,1]} {[1/2,1]}](http://s0.wp.com/latex.php?latex=%7B%5B1%2F2%2C1%5D%7D&bg=ffffff&fg=000000&s=0) ; trên
; trên ![{[0,1/2]} {[0,1/2]}](http://s0.wp.com/latex.php?latex=%7B%5B0%2C1%2F2%5D%7D&bg=ffffff&fg=000000&s=0) bạn dùng ánh xạ
bạn dùng ánh xạ  , trên đoạn
, trên đoạn ![{[1/2,1 ]} {[1/2,1 ]}](http://s0.wp.com/latex.php?latex=%7B%5B1%2F2%2C1+%5D%7D&bg=ffffff&fg=000000&s=0) bạn dùng
bạn dùng  chẳng hạn. Bạn chột dạ và cảm thấy bất ổn vì có quá nhiều cách hợp thành tương tự như thế ; chẳng hạn như bạn hoàn toàn có thể chia đoạn
chẳng hạn. Bạn chột dạ và cảm thấy bất ổn vì có quá nhiều cách hợp thành tương tự như thế ; chẳng hạn như bạn hoàn toàn có thể chia đoạn ![{[0,1]} {[0,1]}](http://s0.wp.com/latex.php?latex=%7B%5B0%2C1%5D%7D&bg=ffffff&fg=000000&s=0) thành hai đoạn
thành hai đoạn ![{[0,1/3]} {[0,1/3]}](http://s0.wp.com/latex.php?latex=%7B%5B0%2C1%2F3%5D%7D&bg=ffffff&fg=000000&s=0) và
và ![{[1/3,1]} {[1/3,1]}](http://s0.wp.com/latex.php?latex=%7B%5B1%2F3%2C1%5D%7D&bg=ffffff&fg=000000&s=0) , hoặc thậm chí bạn có thể chọn hai đoạn bất kỳ trong
, hoặc thậm chí bạn có thể chọn hai đoạn bất kỳ trong ![{[0,1]} {[0,1]}](http://s0.wp.com/latex.php?latex=%7B%5B0%2C1%5D%7D&bg=ffffff&fg=000000&s=0) không có giao, sau đó dùng
không có giao, sau đó dùng 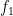 trên đoạn thứ nhất rồi dùng
trên đoạn thứ nhất rồi dùng  trên đoạn thứ hai. Bạn có thể tự chấn an rằng cách đầu tiên có vẻ cân đối nhất nên bạn dùng cách đó mà bỏ qua tất cả các cách hợp thành khác. Thực tế là vẫn không ổn, dù có chọn cách nào thì
trên đoạn thứ hai. Bạn có thể tự chấn an rằng cách đầu tiên có vẻ cân đối nhất nên bạn dùng cách đó mà bỏ qua tất cả các cách hợp thành khác. Thực tế là vẫn không ổn, dù có chọn cách nào thì  cũng khác với
cũng khác với  . Đến đây thì bạn cảm thấy hoang mang thực sự : phạm trù này là loại phạm trù gì khi tiên đề quan trọng nhất là tính kết hợp không được thỏa mãn.
. Đến đây thì bạn cảm thấy hoang mang thực sự : phạm trù này là loại phạm trù gì khi tiên đề quan trọng nhất là tính kết hợp không được thỏa mãn.
Chìa khóa để xua tan sự hoang mang của bạn là : mọi cách hợp thành được nêu ở trên đều tương đương đồng luân với nhau. Nếu bạn thay ánh xạ bằng lớp ánh xạ theo quan hệ tương đương đồng luân, phép hợp thành được xác định một cách duy nhất và tiên đề về tính kết hợp được thỏa mãn. Bạn thở phào, may quá  vẫn là một nhóm.
vẫn là một nhóm.
Bạn đã đủ dũng cảm để hợp thành mũi tên cấp hai chưa. Tôi thì chưa. Tôi chỉ đủ dũng cảm để nghĩ đến các phần tử của nhóm  . Mỗi phần tử là một lớp tương đương đồng luân ánh xạ liên tục từ hình vuông
. Mỗi phần tử là một lớp tương đương đồng luân ánh xạ liên tục từ hình vuông ![{[0,1]^2} {[0,1]^2}](http://s0.wp.com/latex.php?latex=%7B%5B0%2C1%5D%5E2%7D&bg=ffffff&fg=000000&s=0) vào
vào  , nhận giá trị
, nhận giá trị  trên biên của hình vuông. Để hợp thành, tôi khoét trong hình vuông, hai hình vuông nhỏ hơn, không giao nhau. Nếu có hai ánh xạ từ hình vuông vào
trên biên của hình vuông. Để hợp thành, tôi khoét trong hình vuông, hai hình vuông nhỏ hơn, không giao nhau. Nếu có hai ánh xạ từ hình vuông vào 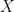 nhận giá trị
nhận giá trị  trên biên, tôi sẽ co chúng lại thành ánh xạ trên hai hình vuông nhỏ rồi thác triển ra toàn bộ hình vuông to bằng cách đặt giá trị
trên biên, tôi sẽ co chúng lại thành ánh xạ trên hai hình vuông nhỏ rồi thác triển ra toàn bộ hình vuông to bằng cách đặt giá trị  lên mọi điểm nằm ở ngoài hai hình vuông nhỏ mà tôi đã khoét. Dĩ nhiên cách hợp thành của tôi phụ thộc vào vị trí của hai hình vuông nhỏ trong hình vuông to, nhưng vì bạn có thể di chuyển thỏa thích hia hình vuông nhỏ trong hình vuông to, hai cách hợp thành khác nhau thực ra tương đương đồng luân với nhau. Như vậy phép hợp thành trong
lên mọi điểm nằm ở ngoài hai hình vuông nhỏ mà tôi đã khoét. Dĩ nhiên cách hợp thành của tôi phụ thộc vào vị trí của hai hình vuông nhỏ trong hình vuông to, nhưng vì bạn có thể di chuyển thỏa thích hia hình vuông nhỏ trong hình vuông to, hai cách hợp thành khác nhau thực ra tương đương đồng luân với nhau. Như vậy phép hợp thành trong  được xác định một cách duy nhất và tiên đề về tính kết hợp được thỏa mãn.
được xác định một cách duy nhất và tiên đề về tính kết hợp được thỏa mãn.
Bạn bất chợt hỏi tôi : cái gì sẽ xảy ra nếu bạn di chuyển hình vuông con thứ nhất vào vị trí của hình vuông con thứ hai và hình vuông con thứ hai về vị trí của hình vuông con thứ nhất sao cho trong quá trình di chuyển, hai hình không bao giờ giao nhau. Tôi nói rằng hoan hô, bạn vừa chứng minh rằng nhóm  là một nhóm giao hóan. Mọi nhóm đồng luân cấp cao
là một nhóm giao hóan. Mọi nhóm đồng luân cấp cao  với
với  đều là nhóm giao hoán.
đều là nhóm giao hoán.
Nhưng bạn cũng đừng chủ quan mà cho rằng vì chũng là nhóm giao hoán nên chắc dễ. Nếu bạn xác định được đồng luân cấp cao của mặt cầu  , sẽ có rất nhiều người ngả mũ chào bạn.
, sẽ có rất nhiều người ngả mũ chào bạn.
Chuyên mục
NGÔ BẢO CHÂU




.jpg)


.jpg)

.jpg)
.jpg)
